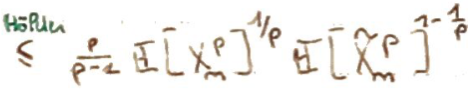Inégalité de Doob dans Lp - Math'φsics

Inégalité de Doob dans Lp

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent
Inégalité de Doob dans \(L^p\) 1) :
\(p\gt 1\)

\((X_n)_n\) est une Sous-martingale positive

\(\tilde X_n:=\displaystyle\max_{k\leqslant n}X_k\)

$$\Huge\iff$$

$${\Bbb E}[\tilde X_n^p]\leqslant\frac p{p-1}{\Bbb E}[X_n^p]$$
Inégalité de Doob dans \(L^p\) 2) :
\(p\gt 1\)

\((M_n)_{n\in\Bbb N}\) est une Martingale positive

\(M_n^*:=\displaystyle\sup_{k\leqslant n}\lvert M_k\rvert\)

$$\Huge\iff$$

$${\Bbb E}[(M_n^*)^p]\leqslant\left(\frac{p}{p-1}\right)^p{\Bbb E}[\lvert M_n\rvert^p]$$
Démontrer \(1)\) :

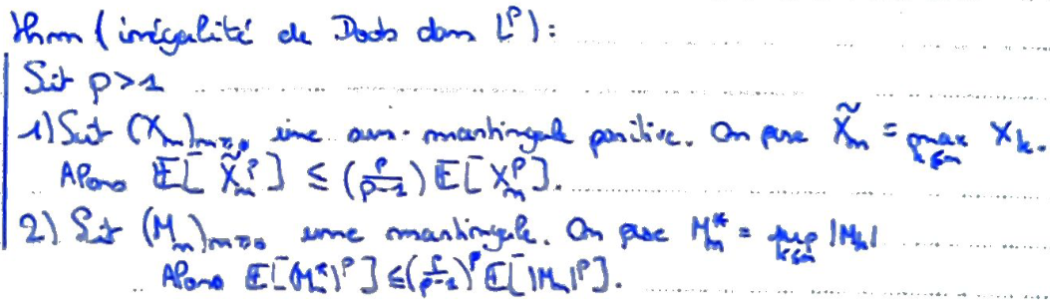
On suppose que le majorant est fini.

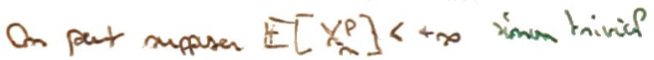
On utilise l'Inégalité de Jensen pour les espérances conditionnelles dans la définition de la martingale montrer que \(k\mapsto{\Bbb E}[X_k^p]\) est croissante.

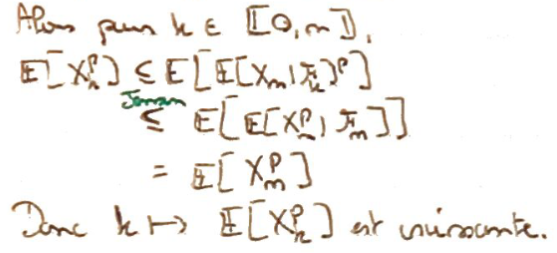
En tant que maximum, on peut majorer \(\tilde X_n\) par la somme des termes, ce qui montre qu'elle est \(\in L^p\).

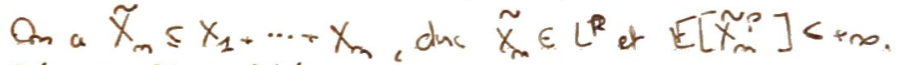
On utilise l'Inégalité maximale de Doob pour majorer.

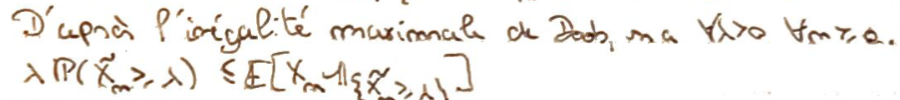
Réécriture sous forme intégrale.

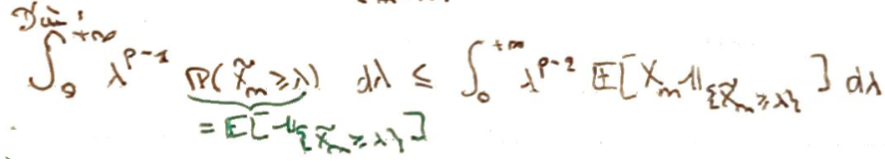
Réorganisation des intégrales par le Théorème de Fubini et résolution.

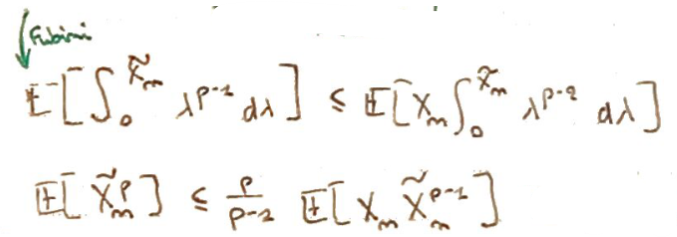
On conclut par Inégalité de Hölder.

Démontrer \(1)\implies2)\) :

Il suffit d'appliquer \(1)\) à \(\lvert M_k\rvert\), qui est une sous-martingale par l'Inégalité de Jensen.
Rétroliens :
- Théorème de Kakutani